Question

Alma is estimating the proportion of students in her school district who, in the past month, read at least 1 book. From a random sample of 50 students, she found that 32 students read at least 1 book last month. Assuming all conditions for inference are met, which of the following defines a 90 percent confidence interval for the proportion of all students in her district who read at least 1 book last month?

a. 32 + or - 1.645 underroot(32)(18)/50.
b. 32 + or - + 1.96 underroot(32)(18)/50.
c. 0.64 + or - 1.282 underroot(0.64)(0.36)/50.
d. 0.64 + or - 1.645 underroot(0.64)(0.36)/50.
e. 0.64 + or - 1.96 underroot(0.64)(0.36)/50.

Answer 1

`0.64 \pm 1.645\sqrt{(0.64*0.36)/(50)}`, option D

Explanation:

In a sample with a number n of people surveyed with a probability of a success of
`\pi`, and a confidence level of
`1-\alpha`, we have the following confidence interval of proportions.

`\pi \pm z\sqrt{(\pi(1-\pi))/(n)}`

In which

z is the zscore that has a pvalue of
`1 - (\alpha)/(2)`.

From a random sample of 50 students, she found that 32 students read at least 1 book last month.

This means that
`n = 50, \pi = (32)/(50) = 0.64`

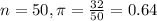
90% confidence level

So
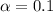`\alpha = 0.1`, z is the value of Z that has a pvalue of
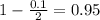`1 - (0.1)/(2) = 0.95`, so
`Z = 1.645`.

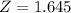Confidence interval:

`\pi \pm z\sqrt{(\pi(1-\pi))/(n)}`

`0.64 \pm 1.645\sqrt{(0.64*0.36)/(50)}`

So the correct answer is given by option D.