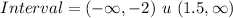Question

-5-4-3

3
The function graphed above is:
Increasing on the interval(s)
Decreasing on the interval(s)

Answer 1

`Interval = (-2,1.5)`

`Interval = (-\infty, -2)\ u\ (1.5,\infty)`

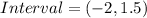
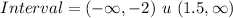
Explanation:

Given

See attachment for graph

Solving (a): Increasing interval

To do this, we simply identify the interval at which the value of the graph increases.

The value has an increased interval between -2 and 1.5 (of the x-axis).

Hence, the increasing interval is:

`Interval = (-2,1.5)`

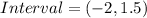
Solving (b): Decreasing interval

To do this, we simply identify the interval at which the value of the graph decreases.

The value has decreased intervals between - infinity and -2 and also 1.5 and infinity (of the x-axis).

Hence, the decreasing interval is:

`Interval = (-\infty, -2)\ u\ (1.5,\infty)`