Question

Find an equation for the perpendicular bisector of the line segment whose endpoints

are (3, 1) and (-9, -5).


Help plz

Answer 1

y= -2x -8

Explanation:

I will be writing the equation of the perpendicular bisector in the slope-intercept form which is y=mx +c, where m is the gradient and c is the y-intercept.

A perpendicular bisector is a line that cuts through the other line perpendicularly (at 90°) and into 2 equal parts (and thus passes through the midpoint of the line).

Let's find the gradient of the given line.

`\boxed{gradient = (y1 -y 2)/(x1 - x2) }`

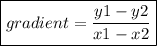
Gradient of given line

`= (1 - ( - 5))/(3 - ( - 9))`

`= (1 + 5)/(3 + 9)`

`= (6)/(12)`

`= (1)/(2)`

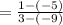
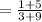
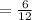
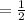
The product of the gradients of 2 perpendicular lines is -1.

(½)(gradient of perpendicular bisector)= -1

Gradient of perpendicular bisector

= -1 ÷(½)

= -1(2)

= -2

Substitute m= -2 into the equation:

y= -2x +c

To find the value of c, we need to substitute a pair of coordinates that the line passes through into the equation. Since the perpendicular bisector passes through the midpoint of the given line, let's find the coordinates of the midpoint.

`\boxed{midpoint = ( (x1 + x2)/(2) , (y1 + y2)/(2)) }`

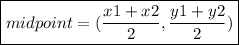
Midpoint of given line

`= ( (3 - 9)/(2) , (1 - 5)/(2) )`

`= ( ( - 6)/(2) , ( - 4)/(2) )`

`= ( - 3 , - 2)`

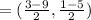
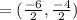
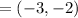
Substituting (-3, -2) into the equation:

-2= -2(-3) +c

-2= 6 +c

c= -2 -6 (-6 on both sides)

c= -8

Thus, the equation of the perpendicular bisector is y= -2x -8.