Question

A plane flying horizontally at an altitude of 3 miles and a speed of 500 mi/h passes directly over a radar station. Find the rate at which the distance from the plane to the station is increasing when it is 4 miles away from the station. (Round your answer to the nearest whole number.)

Answer 1

The rate at which the distance from the plane to the station is increasing is 331 miles per hour.

Explanation:

We can find the rate at which the distance from the plane to the station is increasing by imaging the formation of a right triangle with the following dimensions:

a: is one side of the triangle = altitude of the plane = 3 miles

b: is the other side of the triangle = the distance traveled by the plane when it is 4 miles away from the station and an altitude of 3 miles

h: is the hypotenuse of the triangle = distance between the plane and the station = 4 miles

First, we need to find b:

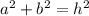`a^(2) + b^(2) = h^(2)` (1)

`b = \sqrt{h^(2) - a^(2)} = \sqrt{(4 mi)^(2) - (3 mi)^(2)} = √(7) miles`

Now, to find the rate we need to find the derivative of equation (1) with respect to time:

`(d)/(dt)(a^(2)) + (d)/(dt)(b^(2)) = (d)/(dt)(h^(2))`

`2a(da)/(dt) + 2b(db)/(dt) = 2h(dh)/(dt)`

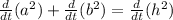
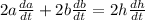
Since "da/dt" is constant (the altitude of the plane does not change with time), we have:

`0 + 2b(db)/(dt) = 2h(dh)/(dt)`

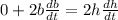
And knowing that the plane is moving at a speed of 500 mi/h (db/dt):

`√(7) mi*500 mi/h = 4 mi*(dh)/(dt)`

`(dh)/(dt) = (√(7) mi*500 mi/h)/(4 mi) = 331 mi/h`

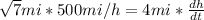
Therefore, the rate at which the distance from the plane to the station is increasing is 331 miles per hour.

I hope it helps you!