Answer:
The rate at which the distance from the plane to the station is increasing is 331 miles per hour.
Explanation:
We can find the rate at which the distance from the plane to the station is increasing by imaging the formation of a right triangle with the following dimensions:
a: is one side of the triangle = altitude of the plane = 3 miles
b: is the other side of the triangle = the distance traveled by the plane when it is 4 miles away from the station and an altitude of 3 miles
h: is the hypotenuse of the triangle = distance between the plane and the station = 4 miles
First, we need to find b:
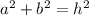 (1)
(1)
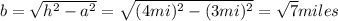
Now, to find the rate we need to find the derivative of equation (1) with respect to time:
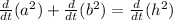
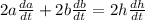
Since "da/dt" is constant (the altitude of the plane does not change with time), we have:
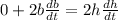
And knowing that the plane is moving at a speed of 500 mi/h (db/dt):
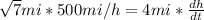
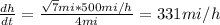
Therefore, the rate at which the distance from the plane to the station is increasing is 331 miles per hour.
I hope it helps you!