Question

You are planning on applying to the Knirhsdaeh institute as a psychology counselor. They hire millions of psychologists around the world. You know the standard deviation for the salaries is $13 k. To find the average, you sample 23 random employees and get an average salary of $81 k. Find an 98% confidence interval for the true average salary of Knirhsdaeh employees.

Answer 1

The 98% of the confidence interval for the true average salary of Knirhsdaeh employees as a psychology counselor

(75.4206, 86.5794)

Explanation:

Step(i):-

Given that the mean of the sample = $81 k

Given that the size of the sample 'n' = 23

Given that the standard deviation for the salaries is $13 k

Step(ii):-

98% of the confidence interval for the true average salary of Knirhsdaeh employees is determined by

`(x^(-) - t_(0.02) (S.D)/(√(n) ) , x^(-) + t_(0.02) (S.D)/(√(n) ))`

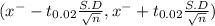
Degrees of freedom = n-1 = 23-1 =22

`t_(0.02) = 2.5083`

`(81 - 2.0583 (13)/(√(23) ) , 81 + 2.0583 (13)/(√(23) ) )`

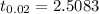
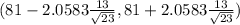
( 81 - 5.57940 , 81 + 5.57940)

(75.4206, 86.5794)

Final answer:-

The 98% of the confidence interval for the true average salary of Knirhsdaeh employees as a psychology counselor

(75.4206, 86.5794)