Answer:
The statement that cushion A is twice as popular as cushion B cannot be verified
Explanation:
From the question we are told that:
Sample size n=38
Type a size A
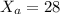
Type a size B
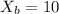
Generally the probability of choosing cushion A P(a) is mathematically given by


Generally the equation for A to be twice as popular as B is mathematically given by
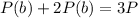
Therefore Hypothesis
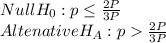
Generally the equation normal approx of p value is mathematically given by
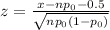
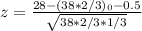
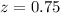
Therefore from distribution table
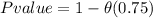
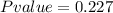
Therefore there is no sufficient evidence to disagree with the Null hypothesis
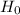
Therefore the statement that cushion A is twice as popular as cushion B cannot be verified