Answer:
The rate of change of the surface area of the sphere is 0.99 cm²/s.
Explanation:
The surface area (A) of a sphere is given by:
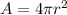
If we derivate the above equation with respect to the time we have:
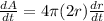
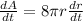 (1)
(1)
Where:
r: is the radius
We need to find
 and r.
and r.
From the volume we can find the radius:
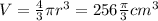
![r = \sqrt[3]{(3V)/(4\pi)} = \sqrt[3]{(3*256*(\pi)/(3))/(4\pi)} = 4 cm](https://img.qammunity.org/2022/formulas/mathematics/college/rbhrt38jri3khs52qoej2v44pph3m1rs3n.png)
And by derivating the volume of the sphere with respect to the time we can calculate
 :
:
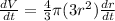


Now, we can calculate the rate of change of the surface area (equation 1):
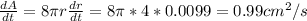
Therefore, the rate of change of the surface area of the sphere is 0.99 cm²/s.
I hope it helps you!