Question

HELP!!! RST has vertices R(-3, - 1), S(0,3), and t(3,0). What type of triangle is RST?

right triangle
Equilateral triangle
scalene triangle
Isosceles

Answer 1

Answer: C) scalene

======================================================

Step-by-step explanation:

Use the distance formula to calculate the distance from R to S. This is identical to the length of segment RS.

`R = (x_1,y_1) = (-3,-1) \text{ and } S = (x_2, y_2) = (0,3)\\\\d = √((x_1 - x_2)^2 + (y_1 - y_2)^2)\\\\d = √((-3-0)^2 + (-1-3)^2)\\\\d = √((-3)^2 + (-4)^2)\\\\d = √(9 + 16)\\\\d = √(25)\\\\d = 5\\\\`

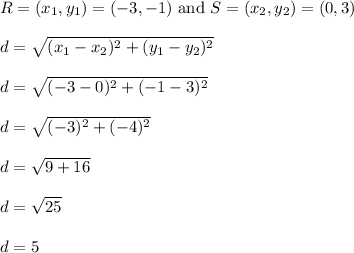
Segment RS is exactly 5 units long.

-----------------------

Repeat similar steps to find the length of segment ST

`S = (x_1,y_1) = (0,3) \text{ and } T = (x_2, y_2) = (3,0)\\\\d = √((x_1 - x_2)^2 + (y_1 - y_2)^2)\\\\d = √((0-3)^2 + (3-0)^2)\\\\d = √((-3)^2 + (3)^2)\\\\d = √(9 + 9)\\\\d = √(18)\\\\d \approx 4.2426\\\\`

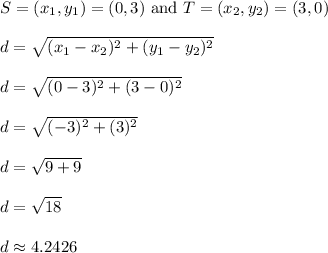
ST is roughly 4.2426 units long.

------------------------

Lastly, let's calculate the length of segment TR.

`T = (x_1,y_1) = (3,0) \text{ and } R = (x_2, y_2) = (-3,-1)\\\\d = √((x_1 - x_2)^2 + (y_1 - y_2)^2)\\\\d = √((3-(-3))^2 + (0-(-1))^2)\\\\d = √((3+3)^2 + (0+1)^2)\\\\d = √((6)^2 + (1)^2)\\\\d = √(36 + 1)\\\\d = √(37)\\\\d \approx 6.0828\\\\`

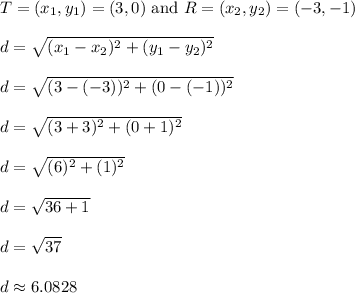
TR is about 6.0828 units long.

------------------------

Summary of the segment lengths:

• RS = 5 exactly
• ST = 4.2426 approximately
• TR = 6.0828 approximately

The three sides are different lengths.

Therefore, the triangle is scalene.