Answer:
Step-by-step explanation:
60000 kJ / h = 60000 x 1000 / (60 x 60 )
= 16667 J /s
a)
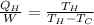
where
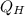 and
and
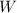 are heat supplied and heat given from outside source .
are heat supplied and heat given from outside source .
Here
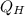 = 16667 J/s
= 16667 J/s
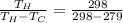
= 15.684
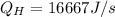
16667 / W = 15.684
W= minimum power supplied = 1062.7 W.
b )
If
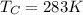
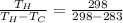
=19.87
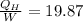
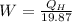
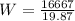
= 838.8 W .