Question

Find the equation of the line using the point-slope formula. Write the final equation using slope-intercept form. Perpendicular to 5y=x-4 and passes through the point (-2,2)

Answer 1

Slope-intercept form: y = -5x - 8

Point-slope form: y - 2 = -5(x + 2)

Explanation:

Given the equation, 5y = x - 4, which passes through point (-2, 2):

Transform the given equation into its slope-intercept form, y = mx + b.

In order to do so, divide both sides by 5 to isolate y:

5y = x - 4

`\displaystyle\mathsf{(5y)/(5)\:=\:(1x\:-\:4)/(5)}`

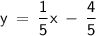`\displaystyle\mathsf{y\:=\:(1)/(5)x\:-\:(4)/(5)}` ⇒ This is the slope-intercept form of 5y = x - 4.

Next, we must determine the equation of the line that is perpendicular to
`\displaystyle\mathsf{y\:=\:(1)/(5)x\:-\:(4)/(5)}`.

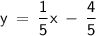Definition of Perpendicular Lines:

Perpendicular lines have negative reciprocal slopes. This means that if we multiply the slopes of two lines, their product will equal to -1.

In other words, if the slope of the given equation is m₁, and the slope of the other line perpendicular to the given linear equation is m₂, then: m₁ × m₂ = -1.

• Slope of the given equation: m₁ = ⅕

• 
  `\displaystyle\mathsf{Slope\:of\:other\:line\:(m_2 )\:=\:-5\:or\:-(5)/(1)}`

If we multiply these two slopes:

• m₁ × m₂ = -1

• 
  `\displaystyle\mathsf{m_1\:*\\\:m_2\:=\:(1)/(5)*\\-(5)/(1)\:=\:-1}`

Now that we have identified the slope of the other line that is perpendicular to 5y = x - 4, we must determine the y-intercept of the other line.

• The y-intercept is the point on the graph where it crosses the y-axis, for which it is the value of "y" when its corresponding x-coordinate equals to zero (0).
• Thus, the standard coordinates of the y-intercept is (0, b), for which its y-coordinate is the value of "b" in the slope-intercept form, y = mx + b.

Using the slope of the other line, m₂ = -5, and the given point, (-2, 2), substitute these values into the slope-intercept form to find the value of the y-intercept, b:

y = mx + b

2 = -5(-2) + b

2 = 10 + b

Subtract 10 from both sides to isolate b:

2 - 10 = 10 - 10 + b

-8 = b

The equation of the other line that is perpendicular to 5y = x - 4 is:

Linear Equation that is perpendicular to 5y = x - 4 in slope-intercept form:

⇒ y = -5x - 8

Rewrite the Equation in Point-slope Form:

The point-slope form is: y - y₁ = m(x - x₁)

In order to rewrite y = -5x - 8 in its point-slope form, we must substitute the value of the given point, (-2, 2) into the point-slope form:

y - y₁ = m(x - x₁)

y - 2 = -5[x - (-2)]

y - 2 = -5(x + 2) ⇒ This is the point-slope form of the line that is perpendicular to 5y = x - 4.