Answer:
Slope-intercept form: y = -5x - 8
Point-slope form: y - 2 = -5(x + 2)
Explanation:
Given the equation, 5y = x - 4, which passes through point (-2, 2):
Transform the given equation into its slope-intercept form, y = mx + b.
In order to do so, divide both sides by 5 to isolate y:
5y = x - 4
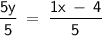
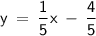 ⇒ This is the slope-intercept form of 5y = x - 4.
⇒ This is the slope-intercept form of 5y = x - 4.
Next, we must determine the equation of the line that is perpendicular to
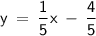 .
.
Definition of Perpendicular Lines:
Perpendicular lines have negative reciprocal slopes. This means that if we multiply the slopes of two lines, their product will equal to -1.
In other words, if the slope of the given equation is m₁, and the slope of the other line perpendicular to the given linear equation is m₂, then: m₁ × m₂ = -1.
- Slope of the given equation: m₁ = ⅕
If we multiply these two slopes:
Now that we have identified the slope of the other line that is perpendicular to 5y = x - 4, we must determine the y-intercept of the other line.
- The y-intercept is the point on the graph where it crosses the y-axis, for which it is the value of "y" when its corresponding x-coordinate equals to zero (0).
- Thus, the standard coordinates of the y-intercept is (0, b), for which its y-coordinate is the value of "b" in the slope-intercept form, y = mx + b.
Using the slope of the other line, m₂ = -5, and the given point, (-2, 2), substitute these values into the slope-intercept form to find the value of the y-intercept, b:
y = mx + b
2 = -5(-2) + b
2 = 10 + b
Subtract 10 from both sides to isolate b:
2 - 10 = 10 - 10 + b
-8 = b
The equation of the other line that is perpendicular to 5y = x - 4 is:
Linear Equation that is perpendicular to 5y = x - 4 in slope-intercept form:
⇒ y = -5x - 8
Rewrite the Equation in Point-slope Form:
The point-slope form is: y - y₁ = m(x - x₁)
In order to rewrite y = -5x - 8 in its point-slope form, we must substitute the value of the given point, (-2, 2) into the point-slope form:
y - y₁ = m(x - x₁)
y - 2 = -5[x - (-2)]
y - 2 = -5(x + 2) ⇒ This is the point-slope form of the line that is perpendicular to 5y = x - 4.