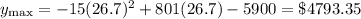Answer:
In order to maximize profit, each widget should sell for $26.70.
Explanation:
The total amount of profit y given by the selling price of each widget x is given by:
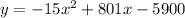
And we want to determine the price of each widget such that is yields the maximum profit.
Since the equation is a quadratic, the maximum profit will occur at the vertex of our parabola.
The vertex of a quadratic is given by:
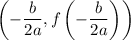
So, let's find the vertex. In our equation, a = -15, b = 801, and c = -5900.
Therefore, the price that maximizes profit is:
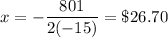
Therefore, in order to maximize profit, each widget should sell for $26.70.
Notes:
Then substituting this back into the equation, the maximum profit is: