Answer:
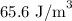
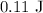
Step-by-step explanation:
B = Magnetic field =

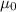 = Vacuum permeability =
= Vacuum permeability =
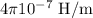
N = Number of turns = 1270
 = Length of solenoid = 93.9 cm = 0.939 m
= Length of solenoid = 93.9 cm = 0.939 m
 = Current = 7.8 A
= Current = 7.8 A
A = Area of solenoid =
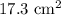
Energy density of a solenoid is given by
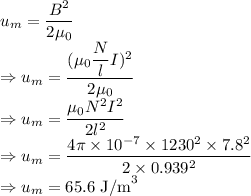
The energy density of the magnetic field inside the solenoid is
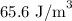
Energy is given by
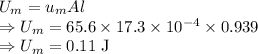
The total energy in joules stored in the magnetic field is
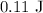 .
.