Answer:
The value of the test statistic and its associated p-value at the 5% significance level are -1.54 and 0.9382, respectively.
Explanation:
A university interested in tracking its honors program believes that the proportion of graduates with a GPA of 3.00 or below is less than 0.16.
This means that the null hypothesis is:
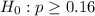
Testing this hypothesis, means that the alternate hypothesis is:
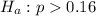
The test statistic is:

In which X is the sample mean,
 is the value tested at the null hypothesis,
is the value tested at the null hypothesis,
 is the standard deviation and n is the size of the sample.
is the standard deviation and n is the size of the sample.
0.16 is tested at the null hypothesis:
This means that
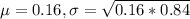
In a sample of 200 graduates, 24 students have a GPA of 3.00 or below.
This means that

Value of the test statistic:

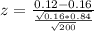
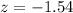
Pvalue:
The pvalue is the probability of finding a sample mean above 0.12, which is 1 subtracted by the pvalue of z = -1.54.
Looking at the z-table, z = -1.54 has a pvalue of 0.0618
1 - 0.0618 = 0.9382
The value of the test statistic and its associated p-value at the 5% significance level are -1.54 and 0.9382, respectively.