Answer:
vf = 9.48 m/s
Step-by-step explanation:
From the law of conservation of energy we can write:
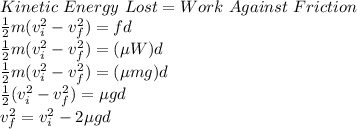
where,
vf = final speed = ?
vi = initial speed = 10.1 m/s
μ = coefficient of friction = 0.3
g = acceleration due to gravity = 9.81 m/s²
d = distance covered = 2.07 m
Therefore,
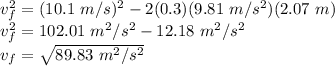
vf = 9.48 m/s