Question

An object of mass 12.9 kg enters a rough floor with speed of 10.1 m/s. The coefficient of friction between the floor and the object is 0.30 and the object moves 2.07 m before returning to a smooth surface (frictionless). What is the velocity of the object once it returns to the smooth surface

Answer 1

vf = 9.48 m/s

Step-by-step explanation:

From the law of conservation of energy we can write:

`Kinetic\ Energy\ Lost = Work\ Against\ Friction\\(1)/(2)m(v_i^2 - v_f^2) = fd\\(1)/(2)m(v_i^2 - v_f^2) = (\mu W)d\\(1)/(2)m(v_i^2 - v_f^2) = (\mu mg)d\\(1)/(2)(v_i^2 - v_f^2) = \mu gd\\v_f^2 = v_i^2 - 2\mu gd`

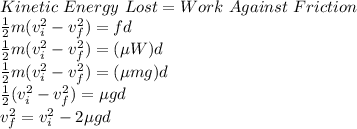
where,

vf = final speed = ?

vi = initial speed = 10.1 m/s

μ = coefficient of friction = 0.3

g = acceleration due to gravity = 9.81 m/s²

d = distance covered = 2.07 m

Therefore,

`v_f^2 = (10.1\ m/s)^2 - 2(0.3)(9.81\ m/s^2)(2.07\ m)\\v_f^2 = 102.01\ m^2/s^2 - 12.18\ m^2/s^2\\v_f = √(89.83\ m^2/s^2)\\`

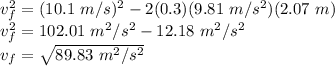
vf = 9.48 m/s