Question

An aircraft component is fabricated from an aluminum alloy that has a plane strain fracture toughness of 30 . It has been determined that fracture results at a stress of 237 MPa when the maximum (or critical) internal crack length is 2.78 mm. a) Determine the value of for this same component and alloy at a stress level of 355 MPa when the maximum internal crack length is 1.39 mm.

Answer 1

fracture will occur since ( 31.8 Mpa√m ) is greater than the
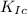`K_{Ic` of the material ( 30 Mpa√m )

Step-by-step explanation:

Given the data in the question;

To determine whether the aircraft component will fracture, given a fracture toughness of 30 Mpa√m, stress level of 355 and maximum internal crack length of 1.39 mm.

On a similar component, it has been said that fracture results at a stress of 237 MPa when the maximum (or critical) internal crack length is 2.78 mm.

so we first of all solve for the parameter Y in the condition where fracture occurred.

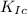`K_{Ic` = 30 Mpa√m

σ = 237 MPa

2α = 2.78 mm = 2.78 × 10⁻³ m

so

Y =
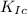`K_{Ic` / σ√πα

we substitute

Y = (30 Mpa√m) / (237 MPa)√(π(2.78 × 10⁻³ m / 2 ) )

Y = (30 Mpa) / (237)( 0.06608187 )

Y = 30 / 15.6614

Y = 1.9155

Next we solve for Yσ√πα for the second case;

σ = 355 Mpa, 2α = 1.39 mm = 1.39 × 10⁻³ m

so

Yσ√πα = 1.9155 × 355 Mpa × √( π × (1.39 × 10⁻³ m / 2) )

= 1.9155 × 355 × 0.0467269

= 31.8 Mpa√m

so

( 31.8 Mpa√m ) >
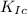`K_{Ic` ( 30 Mpa√m )

Therefore, fracture will occur since ( 31.8 Mpa√m ) is greater than the
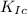`K_{Ic` of the material ( 30 Mpa√m )