This question is incomplete, the missing diagram is uploaded along this answer below.
Answer:
- The mass flow rate of air is 4.59 kg/s
- Area of the exit turbine is 0.066 m²
Step-by-step explanation:
Given the data in the question;
Using air as an ideal gas.
Turbine;
state 1: p₁ = 8 bar, T₁ = 960 K
state 2: p₂ = 1 bar, T₂ = 450 K
The inlet velocity is small compared to the exit velocity of 90 m/s
V₁ < V₂ = 90 m/s
Power of turbine W' = 2500 kW
Now, lets assume Q = 0 and ΔPE = 0
we know that; R = 0.2870 kJ/kg-K
Also.
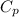 at 700K = 1.075 kJ/kg-K
at 700K = 1.075 kJ/kg-K
Now, using ideal gas law;
STATE1
v₁ = RT₁/p₁
so we substitute
v₁ = [(0.2870 kJ/kg-K)(960 K)/(8 bars )]|
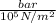 ||
||
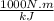 | = 0.344 m³/kg
| = 0.344 m³/kg
STATE2
v₂ = RT₂/p₁
we substitute
v₂ = [(0.2870 kJ/kg-K)(450 K)/(1 bars )]|
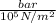 ||
||
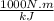 | = 1.2915 m³/kg
| = 1.2915 m³/kg
Now, from energy balance steady state;
0 = Q" - W" +
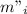 (
(
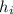 +
+
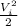 +
+
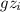 ) -
) -
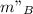 (
(
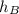 +
+
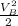 +
+
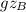 )
)
since we initially assume Q = 0 and ΔPE = 0
hence;
0 =
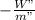 + h₁ +
+ h₁ +
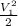 - h₂ +
- h₂ +
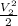
 = h₁ +
= h₁ +
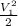 - h₂ +
- h₂ +
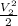
⇒
 =
=
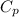 (T₁ - T₂) +
(T₁ - T₂) +
 ( V₁² - V₂²)
( V₁² - V₂²)
we solve for m"
m" = W" / (
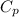 (T₁ - T₂) +
(T₁ - T₂) +
 ( V₁² - V₂²))
( V₁² - V₂²))
so we substitute;
m" = {[2500 kW] / [(1.075kJ/kg-K(960K - 450k) +
 ( (0)² - (90 m/s)²)) |kJ/1000N.m| |N/kg.m/s²|]} | kJ/s / kW|
( (0)² - (90 m/s)²)) |kJ/1000N.m| |N/kg.m/s²|]} | kJ/s / kW|
m" = 4.59 kg/s
Therefore, the mass flow rate of air is 4.59 kg/s
From the mass body steady state;
0 = m"₁ - m"₂
so
m"₁ = m"₂ = 4.59 kg/s
now, the volumetric flow rate V"₂ will be;
V"₂ = m" × v₂
we substitute
V"₂ = 4.59 kg/s × 1.2915 m³/kg = 5.93 m³/s
and
the volumetric flow rate V"₂ = A₂V₂
so;
Exit Area A = V"₂ / V₂
we substitute
A = (5.93 m³/s ) / (90 m/s)
A = 0.06589 ≈ 0.066 m²
Therefore, Area of the exit turbine is 0.066 m²