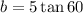Question

Lynn is trying to determine how far away Student B is from the balloon. He decides to use the

equation shown below. Is his equation correct? Why or why not?

5

cos 60º =

BIV x

Answer 1

Did you get the answer If so please give it to me.

Explanation:

Answer 2

See Explanation

Explanation:

The question is incomplete as the image that illustrates the scenario is not given.

However, I can deduce that the question is about a right-angled triangle.

So, I will give a general explanation on how to find each of the side of the triangle, given a side and an angle.

For triangle A (solve for b)

Using cosine formula.

`\cos \theta = (Adjacent)/(Hypotenuse)`

`\cos 60= (5)/(b)`

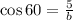
Make b the subject

`b= (5)/(\cos 60)`

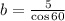
For triangle B (solve for b)

Using cosine formula.

`\sin \theta = (Opposite)/(Hypotenuse)`

`\sin 60= (b)/(5)`

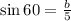
Make b the subject

`b = 5\sin 60`

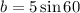
For triangle C (solve for b)

Using cosine formula.

`\tan \theta = (Opposite)/(Adjacent)`

`\tan 60= (b)/(5)`

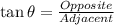
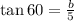
Make b the subject

`b = 5\tan 60`