Question

A student using a stopwatch finds that the time for 10 complete orbits of a ball on the end of a string is 25 seconds. The period of the orbiting ball is​

Answer 1

T = 2.5 s

Step-by-step explanation:

Given that,

Number of complete orbits = 10

Time, t = 25 seconds

We need to find the period of the orbiting ball. Let it is T. We know that number of oscillations per unit time is called frequency and the reciprocal of frequency is called period of the ball.

So,

`T=(t)/(n)\\\\T=(25)/(10)\\\\T=2.5\ s`

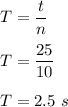
So, the period of the orbiting ball is equal to 2.5 seconds.