Question

A right cylinder has a radius of 7 cm and a height of 3 cm.

Answer the following questions and make sure to *show all your work.*

(a) Find the *Surface Area* of the cylinder

(b) Find the *Volume* of the cylinder

(c) If you wanted more volume in your cylinder, which of these two ideas would give the most *Volume?*
1. Doubling the radius to 14 cm, while the height remains 3 cm.

OR

2. Tripling the height to 9 cm, while the radius remains 7 cm.

Answer 1

V = 141.37 cm³

Surface area = 150.80 cm²

Explanation:

Answer:

V = 141.37 cm³

Surface area = 150.80 cm²

i. Doubling the radius to 6 cm, while the height remains 5

Explanation:

Given that :

Radius, r = 3cm

Height, h = 5cm

Volume, V of right cylinder :

V = πr²h

V = π * 3² * 5

V = 141.37166

V = 141.37 cm³

Surface Area :

2πr(h + r)

2 * π * 3(3 +5)

18.849555(8)

150.79644

= 150.80 cm²

Volume at r = 6 ; h = 5

V = π * 6² * 5

V = 565.48667 cm³

Volume at r = 3 ; h = 15

V = π * 3² * 15

V = 424.11500 cm³

Answer 2

See below

Explanation:

Part A

The surface area of a cylinder is
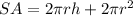`SA=2\pi rh+2\pi r^2` with
`r` being the radius and
`h` being the height:

`SA=2\pi rh+2\pi r^2\\\\SA=2\pi(7)(3)+2\pi(7)^2\\\\SA=2\pi(21)+2\pi(49)\\\\SA=42\pi+98\pi\\\\SA=140\pi`

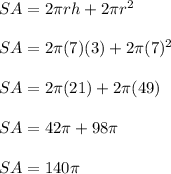
Therefore, the surface area of the given cylinder is 140π cm².

Part B

The volume of a cylinder is
`V=\pi r^2h`:

`V=\pi r^2h\\\\V=\pi (7)^2(3)\\\\V=\pi(49)(3)\\\\V=147\pi`

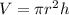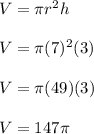
Therefore, the volume of the given cylinder is 147π cm³.

Part C

The first cylinder would have a volume of
`V_1=\pi(14)^2(3)=\pi(196)(3)=588\pi cm^3`

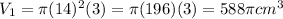
The second cylinder would have a volume of
`V_2=\pi (7)^2(9)=\pi(49)(9)=441\pi cm^3`

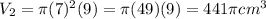
Therefore, the first cylinder with a radius of 14cm and a height of 3cm gives a greater volume of 588π cm³.