Question

Drag each statement to the correct location.

Determine if the given statements are true or false.

The hexadecimal equivalent

of 22210 is DE

The binary equivalent of

D7 is 11010011

The decimal equivalent of

1316 is 19.

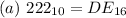True

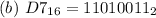False

Answer 1

`(a)\ 222_(10) = DE_(16)` --- True

`(b)\ D7_(16) = 11010011_2` --- False

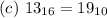`(c)\ 13_(16) = 19_(10)` --- True

Step-by-step explanation:

Required

Determine if the statements are true or not.

`(a)\ 222_(10) = DE_(16)`

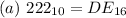
To do this, we convert DE from base 16 to base 10 using product rule.

So, we have:

`DE_(16) = D * 16^1 + E * 16^0`

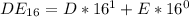
In hexadecimal.

`D =13 \\E = 14`

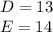
So, we have:

`DE_(16) = 13 * 16^1 + 14 * 16^0`

`DE_(16) = 222_(10)`

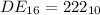
Hence:

(a) is true

`(b)\ D7_(16) = 11010011_2`

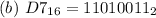
First, convert D7 to base 10 using product rule

`D7_(16) = D * 16^1 + 7 * 16^0`

`D = 13`

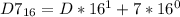
So, we have:

`D7_(16) = 13 * 16^1 + 7 * 16^0`

`D7_(16) = 215_(10)`

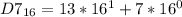
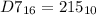
Next convert 215 to base 2, using division rule

`215 / 2 = 107 R 1`

`107/2 =53 R 1`

`53/2 =26 R1`

`26/2 = 13 R 0`

`13/2 = 6 R 1`

`6/2 = 3 R 0`

`3/2 = 1 R 1`

`1/2 = 0 R1`

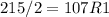
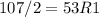
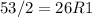
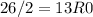
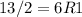
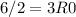
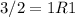
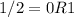
Write the remainders from bottom to top.

`D7_(16) = 11010111_2`

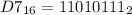
Hence (b) is false

`(c)\ 13_(16) = 19_(10)`

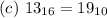
Convert 13 to base 10 using product rule

`13_(16) = 1 * 16^1 + 3 * 16^0`

`13_(16) = 19`

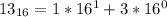
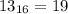
Hence; (c) is true