Question

Simplify the following expression. x(x - 3) - 4(x2 + 7)

Answer 1

`x^(2) -11x-28`

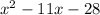
Explanation:

We start of with this.

`x(x-3)-4(2x+7)`

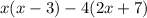
First, use the distributive property, and distribute the x to the (x-3) to get:
`x^(2) -3x-4(2x+7)`

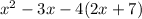
Next, distribute the -4 to the (2x+7) to then get:

`x^(2) -3x-8x-28`

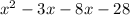
Then, combine like terms. In this case, combine -3x and -8x since they are alike and get:

`x^(2) -11x-28`

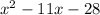
The answer is already in standard form, so we're done. To write a polynomial in standard form, write the monomial with the variable, with the largest exponent first. In this case,
`x^(2)` goes before
`-11x` because of the exponent of 2. Monomials without a variable go last, so that's why -28 is last.

Answer 2

-3x^2 (2 squared) - 3x -28