Answer:
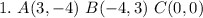 -- Not right triangle
-- Not right triangle
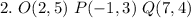 -- Not right triangle
-- Not right triangle
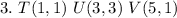 -- Right triangle
-- Right triangle
Step-by-step explanation:
Required
Determine whether the given points make a right triangle
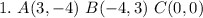
First, calculate the distance between each point using:
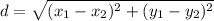
So, we have:
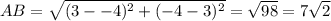
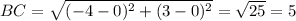
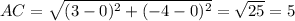
From the above computations, the longest side is AB.
So;
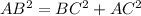 --- Test of Pythagoras
--- Test of Pythagoras
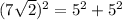
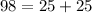
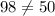
The above points do not make a right triangle
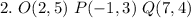
Calculate distance
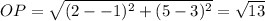
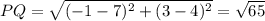
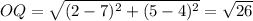
From the above computations, the longest side is PQ
So;
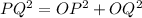 --- Test of Pythagoras
--- Test of Pythagoras
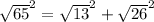
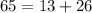
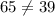
The above points do not make a right triangle
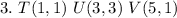
Calculate distance
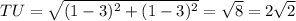
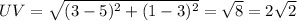
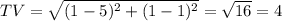
From the above computations, the longest side is TV
So;
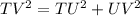 --- Test of Pythagoras
--- Test of Pythagoras
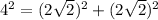
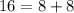
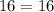
The above points not make a right triangle