Answer:
Explanation:
Slope of line passing through
 and
and
 is given by,
is given by,
m =

From the graph attached,
Slope of the line passing through (-3, 0) and (0, 5) =
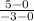
=
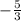
Line passing through a point (h, k) and slope 'm' will be,
y - h = m(x - k)
Since, line passing through (11, 0) is parallel to the line given in the graph,
Slope of the parallel line will be same as
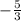
Equation of a line passing through (11, 0) and slope =
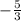
y - 0 =
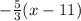
y =
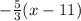
Now satisfy this equation with the points given in the options,
Option (1)
For (1.67, -15.59),
-15.59 =
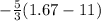
-15.59 = -15.55
False.
Therefore, given point doesn't lie on the line.
Option (2)
For (-0.33, -13.59)
-13.59 =
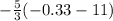
-13.59 = -18.88
False
Option (3)
For (0.67, -18.59),
-18.59 =
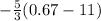
-18.59 = 17.22
False
Option (4)
For (1.67, -15.59)
-15.59 =
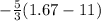
-15.59 = -15.55
False.
Therefore, none of the points given in the options are lying on the line.