Question

1 in

2 in
What is the length of the hypotenuse? If necessary, round to the nearest tenth.

Answer 1

`\boxed {\boxed {\sf c \approx 2.2 \ inches}}`

Explanation:

This triangle has a small square in the corner, representing a right angle. This means we can use the Pythagorean Theorem.

`a^2+b^2=c^2`

Where a and b are the legs and c is the hypotenuse.

In this triangle, the legs are 2 and 1, because they form the right angle. The hypotenuse, which is opposite the right angle, is unknown.

• a = 2
• b=1

Substitute the known values into the formula.

`(2)^2+(1)^2=c^2`

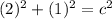
Solve the exponents.

• (2)²= 2*2=4

`4+(1)^2=c^2`

• (1)²=1*1=1

`4+1=c^2`

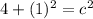
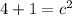
Add.

`5=c^2`

Since we are solving for c, we must isolate the variable. Since it is being squared, we take the square root of both sides.

`\sqrt {5}= √(c^2) \\`

`2.2360679775=c`

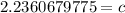
We have to round to the nearest tenth. The 3 in the hundredth place tells us to leave the 2 in the tenths place.

`2.2 \approx c`

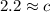
The hypotenuse is approximately 2.2 inches.