Question

GEOMETRY 10TH GRADE NEED HELP ASAP

Answer 1

`\boxed{(6, -3)}`

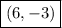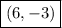
Explanation:

Given the ratio 5:3

and Points A and B where A is located at (-6, 3), and B is located at (26, -13).

Let point A be
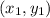`(x_(1), y_(1))`, and let point B be
`(x_(2), y_(2))`.

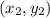(-6, 3) →
`(x_(1), y_(1))`.

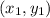(26, -13) →
`(x_(2), y_(2))`.

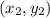Let 5 be n, and 3 be m.

5:3 → n:m

`((nx_(1) + mx_(2))/(n+m), (ny_(1) + my_(2))/(n + m))`.

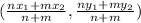To solve, just substitute these variables into the expressions of these coordinates to get the answer.

`((nx_(1) + mx_(2))/(n+m), (ny_(1) + my_(2))/(n + m))` →

`(((5)x_(1) + (3)x_(2))/((5)+(3)), ((5)y_(1) + (3)y_(2))/((5) + (3)))` →

`(((5)(-6)+ (3)(26))/((5)+(3)), ((5)(3)+ (3)(-13))/((5) + (3)))` →

`((-30 + 78)/(8), (15+ -39)/(8))` →

`((78 – 30)/(8), (15 – 39)/(8))` →

`((48)/(8), (-24)/(8))`

→

`((6)/(1), (-3)/(1))`

→

`(6, -3)`.

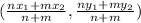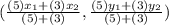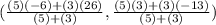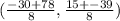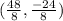
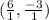
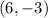Thus the coordinates of B are:

`\boxed{(6, -3)}`

Answer 2

Explanation:

AB:BC::5:3

let the coordinates be (x,y)

`x=(nx1+mx2)/(m+n) \\=(3(-6)+5(26))/(5+3) \\=(-18+130)/(8) \\=(112)/(8) \\=14\\y=(ny1+my2)/(m+n) \\=(3(3)+5(3))/(5+3) \\=(9+15)/(8) \\=(24)/(8) \\=3\\`

coordinates of B are (14,3)