Question

Which of the following is the correct factorization of the polynomial below?

Answer 1

C

Explanation:

p³ - 216q³ ← is a difference of cubes and factors in general as

a³ - b³ = (a - b)(a² + ab + b²) , then

p³ - 216q³

= p³ - (6q)³

= (p - 6q)(p² + 6pq + 36q²) → C

Answer 2

C. (p - 6q)(p² + 6pq + 36q²)

Explanation:

Equation at the end of step 1

`(p^(3) ) - (2^(3) 3^(3) q^(3) )`

Trying to factor as a Difference of Cubes:

Factoring: p^3 - 216q^3

Theory: A difference of two perfect cubes, a^3 - b^3 can be factored into

(a-b) • (a^2 +ab +b^2)

Proof:
`(a-b)(a^(2) +ab+b^(2) ) =`

`a^(3) + a^(2) b+ab^(2) -ba^(2) -b^(2) a-b^(3) =`

`a^(3) +(a^(2) b-ba^(2) )+(ab^(2) -b^(2) a)-b^(3) =`

`a^(3) +0+0-b^(3) =`

`a^(3) -b^(3)`

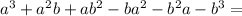
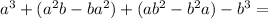
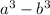
Check: 216 is the cube of 6

Check: p^3 is the cube of p^1

Check: q^3 is the cube of q^1

Factorization is:

`(p-6q)(p^(2) + 6pq+36q^(2) )`

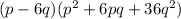
Trying to factor a multi variable polynomial :

Factoring: p^2 + 6pq + 36q^2

Try to factor this multi-variable trinomial using trial and error

Factorization fails

Final Result:

(p - 6q)(p² + 6pq + 36q²)