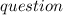
prove that √p is an irrational number , if p is not a perfect square.
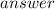
Let us assume, to the contrary, that √p is rational. So, we can find coprime integers a and b(b ≠ 0) such that :-
=> √p = a/b
=> √p b = a
=> pb² = a² ….(i) [Squaring both the sides]
=> a² is divisible by p
=> a is divisible by p So, we can write a = pc for some integer c.
Therefore,
a² = p²c² ….[Squaring both the sides]
=> pb² = p²c² ….[From (i)]
=> b² = pc²
=> b² is divisible by p
=> b is divisible by p
=> p divides both a and b.
=> a and b have at least p as a common factor.
But this contradicts the fact that a and b are coprime. This contradiction arises because we have assumed that √p is rational. Therefore, √p is irrational.
_____________________________________
________________________________