Answer:
Lois will save $152.51 when she wil transfer her balance.
Step-by-step explanation:
Amount to be paid in 1 year for original credit card is given as
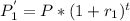
Here
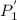 is the amount to be paid after P is the balance which is 970,
is the amount to be paid after P is the balance which is 970,
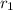 is the APR for first credit card which is 24.2% and t is compounding frequency which is 12 so
is the APR for first credit card which is 24.2% and t is compounding frequency which is 12 so
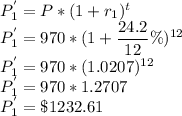
Similarly for the second one the values are calculated as
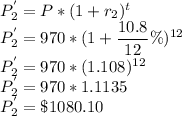
The differnce of the two values is calculated as
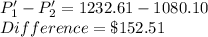
The difference is $152.51 which she could save.