Question

Lois has a balance of $970 on a credit card with an APR of 24.2%, compounded monthly. About how much will she save in interest over the course of the year if she transfers her balance to a credit card with an APR of 10.8%, compounded monthly?

Answer 1

$152.51

Step-by-step explanation:

apeex

Answer 2

Lois will save $152.51 when she wil transfer her balance.

Step-by-step explanation:

Amount to be paid in 1 year for original credit card is given as

`P_1^(')=P*(1+r_1)^t`

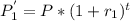
Here
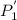`P^(')_1` is the amount to be paid after P is the balance which is 970,
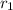`r_1` is the APR for first credit card which is 24.2% and t is compounding frequency which is 12 so

`P_1^(')=P*(1+r_1)^t\\P_1^(')=970*(1+(24.2)/(12)\%)^(12)\\P_1^(')=970*(1.0207)^(12)\\P_1^(')=970*1.2707\\P_1^(')=\$1232.61`

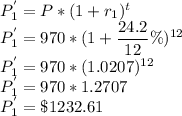
Similarly for the second one the values are calculated as

`P_2^(')=P*(1+r_2)^t\\P_2^(')=970*(1+(10.8)/(12)\%)^(12)\\P_2^(')=970*(1.108)^(12)\\P_2^(')=970*1.1135\\P_2^(')=\$1080.10`

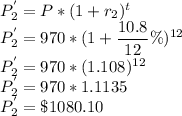
The differnce of the two values is calculated as

`P_1'-P_2'=1232.61-1080.10\\Difference=\$ 152.51`

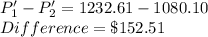
The difference is $152.51 which she could save.