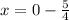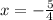Question

A parabola is represented by the equation y2 = 5x. Which equation represents the directrix? Y = –20 x = –20 y = Negative five-fourths x = Negative five-fourths

Answer 1

D on edg 2021

Step-by-step explanation:

yoiuuiy

Answer 2

`x = - (5)/(4)`

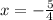
Step-by-step explanation:

Given

`y^2 = 5x`

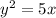
Required

Determine the directrix

First, we express the equation in form:

`(y - k)^2 = 4p (x - h)`

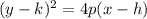
Where the directrix is:

`x = h - p`

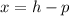
So, we have:

`y^2 = 5x`

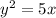
Rewrite as:

`(y - 0)^2 = 5(x - 0)`

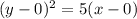
Multiply the right hand side by 4/4

`(y - 0)^2 = (4)/(4) * 5(x - 0)`

`(y - 0)^2 = 4* (5)/(4) (x - 0)`

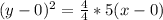
By comparison:

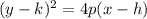`(y - k)^2 = 4p (x - h)` and
`(y - 0)^2 = 4* (5)/(4) (x - 0)`

`k = 0`

`p =(5)/(4)`

`h = 0`

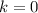
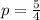
The directrix is calculated as:

`x = h - p`

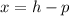
So:

`x = 0 - (5)/(4)`

`x = - (5)/(4)`