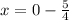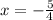Answer:
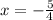
Step-by-step explanation:
Given
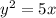
Required
Determine the directrix
First, we express the equation in form:
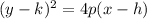
Where the directrix is:
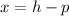
So, we have:
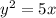
Rewrite as:
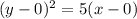
Multiply the right hand side by 4/4
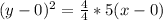
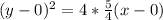
By comparison:
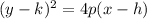 and
and
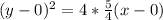
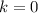
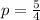
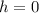
The directrix is calculated as:
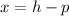
So: