Question

This set of ordered pairs shows a relationship between x and y. {(0, -2), (3, 7), (6, 16), (6, 15), (8, 21), (10, 28), (11,31)} Using the line of best fit, which is closest to the output when the input is 5?

Answer 1

The closest to the output when the input is approximately 12

Explanation:

The given (x, y) coordinates are;

The line of best fit is

x, 0, 3, 6, 6, 8, 10, 11

y, -2, 7, 16, 15, 21, 28, 31

The line of best fit can be obtained from the scatter plot of the given data from where a linear pattern is apparent

A linear line of best fit is a trend line that gives an overall cumulative minimum distance of all the points from the line

The method for constructing a line of best fit includes;

1) The least Squares Method

2) The method of linear regression

3) Construction of line of best fit

a) The area method

b) The dividing method

The least squares equation is given as follows;

`\hat y` = a + b·x

`b = (\Sigma (x_i - \overline x) \cdot (y_i - \overline y))/(\Sigma (x_i - \overline x)^2 )`

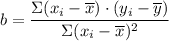
From MS Excel, we have;

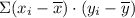`{\Sigma (x_i - \overline x) \cdot (y_i - \overline y)}{ }` = 266.8571

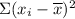`{\Sigma (x_i - \overline x)^2 }` = 89.42857

∴ b = 266.8571/89.42857 ≈ 2.984

`a =\overline y- b \cdot \overline x`

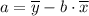
From MS Excel, with the given data, we get;

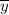`\overline y` = 16.57143

`\overline x` = 6.285714

Therefore;

a = 16.57143 - 2.984 × 6.285714 = -2.185

Therefore, we get the following regression equation;

`\hat y` = -2.185 + 2.9·x

Where;

x = The input

`\hat y` = The output

Therefore, when x = 5, we get;

`\hat y` = -2.185 + 2.9 × 5 = 12.315

Therefore, the closest to the output when the input is 5, y ≈ 12