Question

One airplane is approaching an airport from the north at 164 km/hr. A second airplane approaches from the east at 271 km/hr. Find the rate at which the distance between the planes changes when the southbound plane is 28 km away from the airport and the westbound plane is 17 km from the airport.

Answer 1

The rate of change of the distance between the airplanes is approximately 316.760 kilometers.

Explanation:

The distance between both airplanes (r), in kilometers, can be determined by the Pythagorean Theorem, that is:

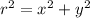`r^(2) = x^(2)+y^(2)` (1)

Where:

`x` - Distance of the westbound airplane from airport, in kilometers.

`y` - Distance of the southbound airplane from airport, in kilometers.

By Differential Calculus, we derive an expression for the rate of change of the distance between the airplanes (
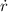`\dot r`), in kilometers per hour:

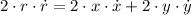
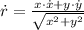`2\cdot r\cdot \dot r = 2\cdot x \cdot \dot x + 2\cdot y \cdot \dot y`

`\dot r = \frac{x\cdot \dot x + y\cdot \dot y}{\sqrt{x^(2)+y^(2)}}` (2)

Where:

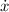`\dot x` - Rate of change of the distance of the westbound airplane, in kilometers per hour.

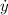`\dot y` - Rate of change of the distance of the southbound airplane, in kilometers per hour.

If we know that
`x = 17\,km`,
`y = 28\,km`,
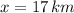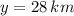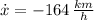`\dot x = -164\,(km)/(h)` and
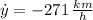`\dot y = -271\,(km)/(h)`, then the rate of change of the distance between the airplanes is:

`\dot r = \frac{x\cdot \dot x + y\cdot \dot y}{\sqrt{x^(2)+y^(2)}}`

`\dot r \approx -316.760\,km`

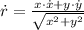
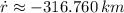
The rate of change of the distance between the airplanes is approximately 316.760 kilometers.