Answer:
The production cost for a packet of super tea is 924.
Explanation:
The production cost of the Super tea is given as

Here the costs are given as following
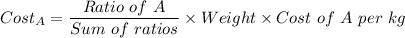
Here
- Ratio of A is 1.5
- Sum of Ratios is 1.5+5+1=7.5
- Weight is 825 g or 0.825kg
- Cost of A per kg is 1600
So
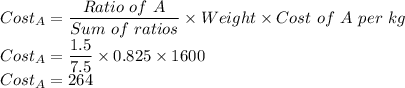
The cost of A is 264.
Similarly
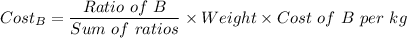
Here
- Ratio of B is 5
- Sum of Ratios is 7.5
- Weight is 825 g or 0.825kg
- Cost of B per kg is 800
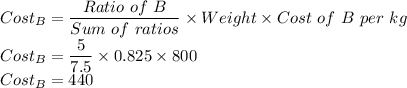
The cost of B is 440.
Also
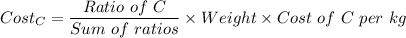
Here
- Ratio of C is 1
- Sum of Ratios is 7.5
- Weight is 825 g or 0.825kg
- Cost of C per kg is 1700
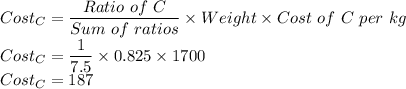
The cost of C is 187.
Now the packaging and blending cost for the given package is calculated as
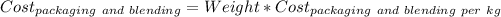
Here
- Weight is 825 g or 0.825kg
- Cost of packaging and blending per kg is 40
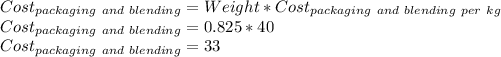
Cost of packaging and blending per packet is 33.
So now substituting values of costs in the following equation gives:
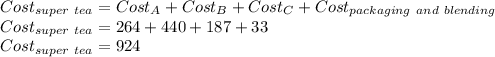
The production cost for a packet of super tea is 924.