Question

A company that manufactures electronic components wants to know the mean discharge time of one particular type of capacitor that it makes. In order to estimate this value, they randomly select 100 capacitors and measure how long they take to discharge. The mean of this sample was 7.25 seconds with a standard deviation of 0.15 seconds. Assuming that this distribution is normal, construct a 99% confidence interval to estimate the mean discharge time for all capacitors of this type. Is this question asking for a confidence interval or hypothesis test

Answer 1

99% confidence interval to estimate the mean discharge time for all capacitors of this type

(7.2146, 7.2854)

Explanation:

Step(i):-

Given that the sample size 'n' = 100

Given that the mean of sample x⁻ = 7.25 seconds

Given that the standard deviation of the sample (S) = 0.15 seconds

Level of significance = 0.01

Degrees of freedom = n-1 =100-1 =99

t₀.₀₁ , ₉₉ = 2.3646

We have to find that the 99% of the confidence interval of the mean

Step(ii):-

99% confidence interval to estimate the mean discharge time for all capacitors

`(x^(-) - t_(0.01 , 99) (S)/(√(n) ) , x^(-) + t_(0.01 , 99) (S)/(√(n) ) )`

`(7.25 - 2.3646 (0.15)/(√(100) ) , 7.25 + 2.3646 (0.15)/(√(100) ) )`

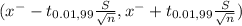
(7.25 - 0.0354 , 7.25 + 0.0354)

(7.2146, 7.2854)

Final answer:-

99% confidence interval to estimate the mean discharge time for all capacitors of this type

(7.2146, 7.2854)