Question

Given the sequence
`c_n` defined recursively below, find
`c_5`.


`c_1 =4`

`c_2 = 2`

`c_n = 3c_(n-1)+2c_(n-2)-2`

Answer 1

Now we have to,

find the required value of c₅.

Given that,

→ c₁ = 4

→ c₂ = 2

→
`\sf {c_n = 3c_(n-1)+2c_(n-2)-2}`

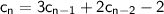
Let's solve c₃ first,

→ 3c₂ + 2c₁ - 2

→ 3(2) + 2(4) - 2

→ 6 + 8 - 2 = 12

Then the value of c₃ is

→ [c₃ = 12]

Then find the value of c₄,

→ c₄ = 3(12) + 2(2) - 2

→ c₄ = {36 + 4} - 2

→ c₄ = 40 - 2

→ [c₄ = 38]

Next we can solve for c₅,

→ c₅ = 3(38) + 2(12) - 2

→ c₅ = {114 + 24} - 2

→ c₅ = 138 - 2

→ [c₅ = 136]

Hence, the value of c₅ is 136.

Answer 2

Hello!

`\large\boxed{c_(5) = 136}`

We can begin by solving for c₃ given the equations:

c₃ = 3c₂ + 2c₁ - 2

c₃ = 3(2) + 2(4) - 2

Simplify:

c₃ = 6 + 8 - 2 = 12

We can now find the subsequent terms:

c₄ = 3(12) + 2(2) - 2 = 38

c₅ = 3(38) + 2(12) - 2 = 136