Answer:
The estimated standard error is
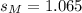 .
.
The t statistic is
 .
.
Explanation:
The test statistic is:
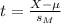
In which X is the sample mean,
 is the value tested at the null hypothesis,
is the value tested at the null hypothesis,
 is the standard error, s is the standard deviation and n is the size of the sample.
is the standard error, s is the standard deviation and n is the size of the sample.
The average duration of labor from the first contraction to the birth of the baby in women over 35 who have not previously given birth and who did not use any pharmaceuticals is 16 hours.
This means that
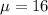
Suppose you have a sample of 35 women who exercise daily, and who have an average duration of labor of 16.9 hours and a sample variance of 39.7 hours.
This means that
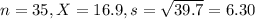
The estimated standard error is:
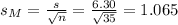
The estimated standard error is
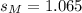 .
.
Calculate the t statistic.
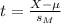
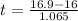

The t statistic is
