Answer:
95% of the confidence interval for the proportion of smokers who have tried to quit within the past year
(0.47228 , 0.49868)
Explanation:
Step(i):-
Given that the National Center for Health Statistics interviewed 5409 adult smokers in 2015
and 2626 of them said they had tried to quit smoking during the past year
proportion
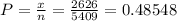
Q = 1-P = 1 - 0.48548 = 0.5146
Step(ii):-
95% of the confidence interval for the proportion of smokers who have tried to quit within the past year
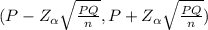
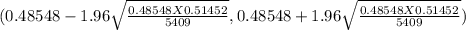
( 0.48548 - 0.0132 , 0.48548 +0.0132)
(0.47228 , 0.49868)
Final answer:-
95% of the confidence interval for the proportion of smokers who have tried to quit within the past year
(0.47228 , 0.49868)