Question

Assume that all​ grade-point averages are to be standardized on a scale between 0 and 6. How many​ grade-point averages must be obtained so that the sample mean is within 0.013 of the population​ mean? Assume that a ​98% confidence level is desired. If using the range rule of​ thumb, σ can be estimated as range/4=(6-0)/2=1.5. Does the sample size seem​ practical?

Answer 1

The sample size 'n' = 72,030

Explanation:

Step(i):-

Given that the Estimate Error = 0.013

Given that the standard deviation of the Population = 1.5

The estimated error is determined by

`E = (Z_(0.98) S.D )/(√(n) )`

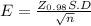
Step(ii):-

Given that the Level of significance = 0.98 or 0.02

Z₀.₀₂ = 2.326

The estimated error is determined by

`E = (Z_(0.98) S.D )/(√(n) )`

`0.013 = (2.326 X 1.5 )/(√(n) )`

`√(n) = (3.489)/(0.013) = 268.38`

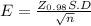
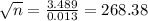
Squaring on both sides, we get

n = 72,030

Final answer:-

The sample size 'n' = 72,030