Answer:
The sample size 'n' = 72,030
Explanation:
Step(i):-
Given that the Estimate Error = 0.013
Given that the standard deviation of the Population = 1.5
The estimated error is determined by
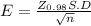
Step(ii):-
Given that the Level of significance = 0.98 or 0.02
Z₀.₀₂ = 2.326
The estimated error is determined by
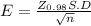
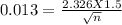
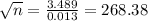
Squaring on both sides, we get
n = 72,030
Final answer:-
The sample size 'n' = 72,030