Answer:
The speed of the knife after passing through the target is 9.33 m/s.
Step-by-step explanation:
We can find the speed of the knife after the impact by conservation of linear momentum:
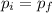
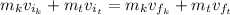
Where:
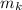 : is the mass of the knife = 22.5 g = 0.0225 kg
: is the mass of the knife = 22.5 g = 0.0225 kg
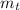 : is the mass of the target = 300 g = 0.300 kg
: is the mass of the target = 300 g = 0.300 kg
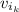 : is the initial speed of the knife = 40.0 m/s
: is the initial speed of the knife = 40.0 m/s
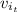 : is the initial speed of the target = 2.30 m/s
: is the initial speed of the target = 2.30 m/s
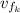 : is the final speed of the knife =?
: is the final speed of the knife =?
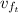 : is the final speed of the target = 0 (it is stopped)
: is the final speed of the target = 0 (it is stopped)
Taking as a positive direction the direction of the knife movement, we have:
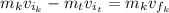
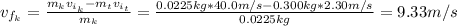
Therefore, the speed of the knife after passing through the target is 9.33 m/s.
I hope it helps you!