Question

A knife thrower throws a knife toward a 300 g target that is sliding in her direction at a speed of 2.30 m/s on a horizontal frictionless surface. She throws a 22.5 g knife at the target with a speed of 40.0 m/s. The target is stopped by the impact and the knife passes through the target. Determine the speed of the knife (in m/s) after passing through the target.

Answer 1

The speed of the knife after passing through the target is 9.33 m/s.

Step-by-step explanation:

We can find the speed of the knife after the impact by conservation of linear momentum:

`p_(i) = p_(f)`

`m_(k)v_{i_(k)} + m_(t)v_{i_(t)} = m_(k)v_{f_(k)} + m_(t)v_{f_(t)}`

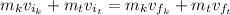
Where:

`m_(k)`: is the mass of the knife = 22.5 g = 0.0225 kg

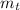`m_(t)`: is the mass of the target = 300 g = 0.300 kg

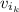`v_{i_(k)}`: is the initial speed of the knife = 40.0 m/s

`v_{i_(t)}`: is the initial speed of the target = 2.30 m/s

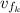`v_{f_(k)}`: is the final speed of the knife =?

`v_{f_(t)}`: is the final speed of the target = 0 (it is stopped)

Taking as a positive direction the direction of the knife movement, we have:

`m_(k)v_{i_(k)} - m_(t)v_{i_(t)} = m_(k)v_{f_(k)}`

`v_{f_(k)} = \frac{m_(k)v_{i_(k)} - m_(t)v_{i_(t)}}{m_(k)} = (0.0225 kg*40.0 m/s - 0.300 kg*2.30 m/s)/(0.0225 kg) = 9.33 m/s`

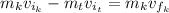
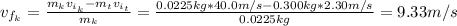
Therefore, the speed of the knife after passing through the target is 9.33 m/s.

I hope it helps you!