Answer:
g = 1.19 m / s²
Step-by-step explanation:
Let's solve this problem in parts.
Let's start by looking for the speed of the pulse in the wire, the wave speed is constant
v = l / t
let's calculate
v = 1.52 / 0.0833
v = 18.25 m / s
now we can use the relationship between velocity and material properties
v =
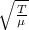
T = v² μ
let's calculate
T = 18.25² 4.41 10-4
T = 1.4688 10-1 N
finally let's use the equilibrium condition
T - W = 0
W = T
m g = T
g = T / m
we calculate
g = 1.4688 10⁻¹ / 0.123
g = 1.19 m / s²