Question

In this experiment researchers randomly assigned smokers to treatments. Of the 193 smokers taking a placebo, 29 stopped smoking by the 8th day. Of the 266 smokers taking only the antidepressant buproprion, 82 stopped smoking by the 8th day. Calculate the estimated standard error for the sampling distribution of differences in sample proportions.

Answer 1

The estimated standard error for the sampling distribution of differences in sample proportions is 0.0382.

Explanation:

To solve this question, we need to understand the Central Limit Theorem and subtraction of normal variables.

Central Limit Theorem

The Central Limit Theorem estabilishes that, for a normally distributed random variable X, with mean
`\mu` and standard deviation
`\sigma`, the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean
`\mu` and standard deviation
`s = (\sigma)/(√(n))`.

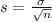For a skewed variable, the Central Limit Theorem can also be applied, as long as n is at least 30.

For a proportion p in a sample of size n, the sampling distribution of the sample proportion will be approximately normal with mean
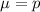`\mu = p` and standard deviation
`s = \sqrt{(p(1-p))/(n)}`

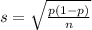
Subtraction of normal variables:

When we subtract normal variables, the mean is the subtraction of the means, while the standard error is the square root of the sum of the variances:

Of the 193 smokers taking a placebo, 29 stopped smoking by the 8th day.

This means that:

`p_S = (29)/(193) = 0.1503`

`s_S = \sqrt{(0.1503*0.8497)/(193)} = 0.0257`

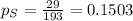
Of the 266 smokers taking only the antidepressant buproprion, 82 stopped smoking by the 8th day.

This means that:

`p_A = (82)/(266) = 0.3083`

`s_A = \sqrt{(0.3083*0.6917)/(266)} = 0.0283`

Calculate the estimated standard error for the sampling distribution of differences in sample proportions.

`s = √(s_S^2 + s_A^2) = √(0.0257^2 + 0.0283^2) = 0.0382`

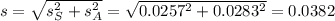
The estimated standard error for the sampling distribution of differences in sample proportions is 0.0382.