Question

Pleaseee helppp with thisss asappp

Answer 1

We are given with a equation of Circle and we need to find it's radius and it's equation in standard form . But , let's recall , the standard equation of a circle is
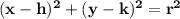`{\bf (x-h)^(2)+(y-k)^(2)=r^(2)}` where (h,k) is the centre of the circle and radius is r . Proceeding further ;

`{:\implies \quad \sf x^(2)+12y+22x+y^(2)-167=0}`

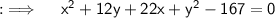
Collecting x terms , y terms and transposing the constant to RHS ;

`{:\implies \quad \sf (x^(2)+22x)+(y^(2)+12y)=167}`

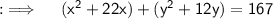
Now , as in standard equation their is a whole square , so we need to develop a whole square in LHS , for which we will use completing the square method , as coefficient of x² and y² is 1 , so adding 121 and 36 to LHS and RHS .

`{:\implies \quad \sf (x^(2)+22x+121)+(y^(2)+12y+36)=167+121+36}`

`{:\implies \quad \sf (x+11)^(2)+(y+6)^(2)=324\quad \qquad \{\because a^(2)+2ab+b^(2)=(a+b)^(2)\}}`

`{:\implies \quad \bf \therefore \quad \underline{\underline{\{x-(-11)\}^(2)+\{y-(-6)\}^(2)=(18)^(2)}}}`

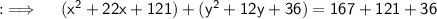
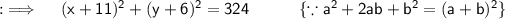
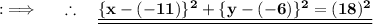
On comparing this with the standard equation , we got our centre at (-11,-6) and radius is 18 units