Answer:
Question (a)
Midpoint of a line segment:
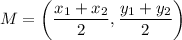
Given:
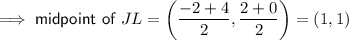
Given:
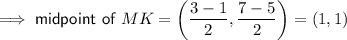
Question (b)
Find slopes (gradients) of JL and MK then compare. If the product of the slopes of JL and MK equal -1, then JL and MK are perpendicular.
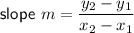
Given:
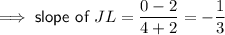
Given:
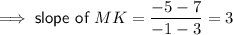
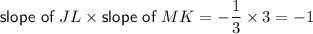
Hence segments JL and MK are perpendicular