Given:
The quadratic equation is:
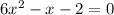
To find:
The nature of the solutions by using the discriminant.
Solution:
If a quadratic equation is
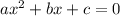 , then its discriminant is:
, then its discriminant is:
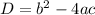
If D<0, then both roots are complex.
If D=0, then both roots are real and equal.
If D>0, then both roots are real and distinct.
We have,
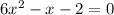
Here,
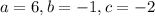 . So, the value of the discriminant is:
. So, the value of the discriminant is:
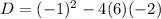
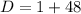
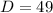
Since
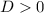 , then both roots are real and distinct.
, then both roots are real and distinct.
Hence, the discriminant of the given quadratic equation is 49 and both roots are real and distinct.